Violin making and AI: Intelligent design

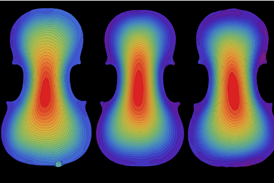
The idea that the shape and thickness of a violin’s top and back plates can affect its sound is nothing new. Antonio Stradivari was undoubtedly aware of it 300 years ago, and the science behind it was scrutinised and written up at length by Carleen Hutchins in the 1950s. Since then, the phenomenon of violin ‘modes’ and resonances has been investigated by both violin makers and academics; indeed, for many luthiers, one of the first steps in making a new instrument will be to examine its ‘tap tones’, or speed of sound along the plates. But what if we could predict how an instrument will sound even before we build it? Could it be possible for modern technology to give an idea of the final plates’ vibrational behaviour, and even understand how a good violin could be made to sound ‘great’?

A team from the Politecnico di Milano’s musical acoustic laboratory has recently completed a project using artificial intelligence (AI) software to examine violin forms. The study demonstrates that a simple neural network can learn to predict the way a violin’s top plate will vibrate, just from parameters relating to its geometry and material. For this project, we took a fundamentally different approach from the standard method of investigation – which, in a nutshell, is ‘varying X while leaving everything else constant’. In other words, you start with a model of a violin, vary one parameter at a time, and see how the instrument’s eigenfrequencies change as a result of varying that one parameter. The eigenfrequency (or ‘modal frequency’) is the frequency at which a system tends to oscillate in the absence of any driving or damping force, and the shape this vibration has in space is called the ‘normal mode’. These modes can be understood by analogy to the vibrations of a string, where the fundamental is always accompanied by several harmonics: these are the normal modes of a string…